Saya lagi belajar tentang aksioma probabilitas. Di matematika teori dapat dikembangkan dari aksioma. Aksioma itu adalah aturan dasar atau prinsip yang dijadikan sandaran teori matematika berikutnya. Dari aksioma diturunkan menjadi teori berdasarkan bukti (proof) melalui logika deduktif.
Contohnya dalam teori probabilitas, kita bisa turunkan keseluruhan teori hanya dari 3 aksioma. Pendekatan aksioma ini berguna misalnya untuk memastikan bahwa sebuah teori konsisten dan tidak bertentangan dengan teori lainnya. Aksioma dapat juga kita program di komputer, dan digunakan untuk menyelesaikan permasalahan riil lainnya.
Selain teori dan aksioma, biasanya ada juga definisi. Definisi membangun konsep baru dari konsep yang sudah ada. Konsep yang sudah ada pada axioma. Definisi tidak memberikan asumsi baru ke teori, namun menjelaskan aksioma.
Jadi ada 3 macam pernyatan.
- Aksioma: Prinsip dasar yang kita terima kebenarannya
- Definisi: Pernyataan yang mengenalkan konsep baru
- Teori: Pernyataan yang diturunkan dari aksioma dan definisi
3 Aksioma Probabilitas
Teori Probabilitas memiliki 3 aksioma, yaitu:
- Normality: 0<=P(A)<=1
- Tautology rule: P(True) = 1 ; P(False)=0
- Additivity rule : P(A or B) = P(A) + P(B) – P(A and B)
Dari 3 aksioma ini kemudian dapat kita turunkan berbagai teori probabilitas. Yang pertama adalah Rule Negasi:
P(A’)=1-P(A)
Contradiction Rule
Bila A adalah kontradiksi maka P(A)=0
Conditional Probability
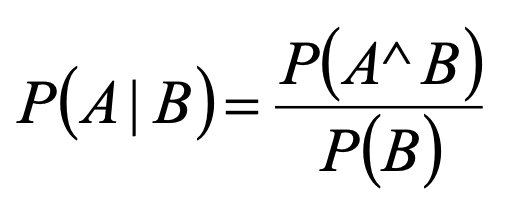
Multiplication Rule:
Bila P(B)>0 maka P(A and B) = P(A|B) P(B)
Equivalent Rule:
Jika A & B logical equivalent maka P(A)=P(B)
General Addition Rule
P(A or B) = P(A) + P(B) – P(A and B)
Total Probability rule:
Jika 0< P(B) < 1 maka P(A) = P (A|B) P(B) + P(A|B’) P(B’)
Teori Bayes
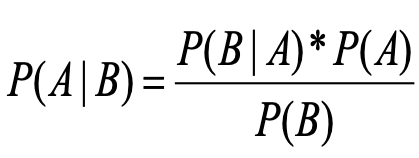
Versi Panjang:
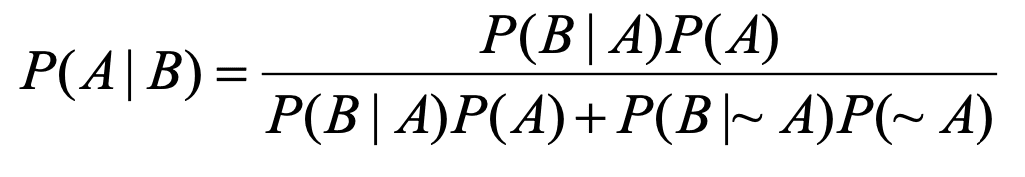
Independensi:
A independen dari B jika P(A|B) = P(A) dan P(A) > 0
Jika A independen dari B, maka P (A and B) = P(A) P(B)
Jika A independen dari B, maka B independen dari A
Semoga Bermanfaat!
diterjemahkan dari:
https://jonathanweisberg.org/vip/the-axioms-of-probability.html