Bayes Net sering disebut sebagai model-model grafik. Ide utamanya adalah menggunakan asumsi conditional independence. Prinsip ini sudah digunakan juga di Naive Bayes (NB). Manfaatnya adalah membuat perhitungan probabilitas menjadi sederhana. Dengan NB kita hanya perlu 2n+1 parameter. Sementara pake Bayes rules dibutuhkan 2^n. Namun asumsi NB ini cukup ekstrem karena menyamaratakan semua conditional independensi dari semua atribut yang terlibat.
Bayesnet sedikit menetralisir permasalahan tersebut. Kalau kita mempunyai pengetahuan tambahan keterkaitan antara satu variabel dengan variabel lainnya, maka bisa dimasukan dalam perhitungan. Sehingga bisa dikatakan Bayesnet berada ditengah antara NB dan Bayes rules. Keterkaitan hubungan ini dibuat dalam bentuk graph. Graph ini menunjukan joint probability distribution dari sekumpulan variabel/nodes.
Ada 2 tipe model graph: yaitu directed graph (yang digunakan pada bayesnet) dan yang undirected graph (tidak terarah seperti markov random fields)
Model Graph ini memasukan pengetahuan kita tentang domain dalam bentuk dependensi atau independensi. Serta mengamati data untuk melakukan estimasi parameter. Model Graphs ini adalah salah satu perkembangan Machine Learning yang penting. Prinsip model graph ini digunakan untuk probabilistic inference dan learning (pembelajaran). Metode ini digunakan pada analisa teks, model time series, diagnosa, sistem bantuan (help system) dll.
X disebut conditional independen terhadap Y|Z bila distribusi probabiliti X tidak bergantung pada Y
P(X|Y,Z)=P(X|Z)
contohnya P(Guntur|Hujan, Kilat)= P(Guntur|Kilat)
X independen secara marginal terhadap Y bila Probabiliti kemunculan X dan Y dinyatakan sebagai perkalian probabiliti X dan Y:
P(X=xi|Y=yj) = P(X=xi)
P(Y=yi|X=xj) = P(Y=yi)
Contoh hubungan joint probability distribution terhadap variabel berikut:
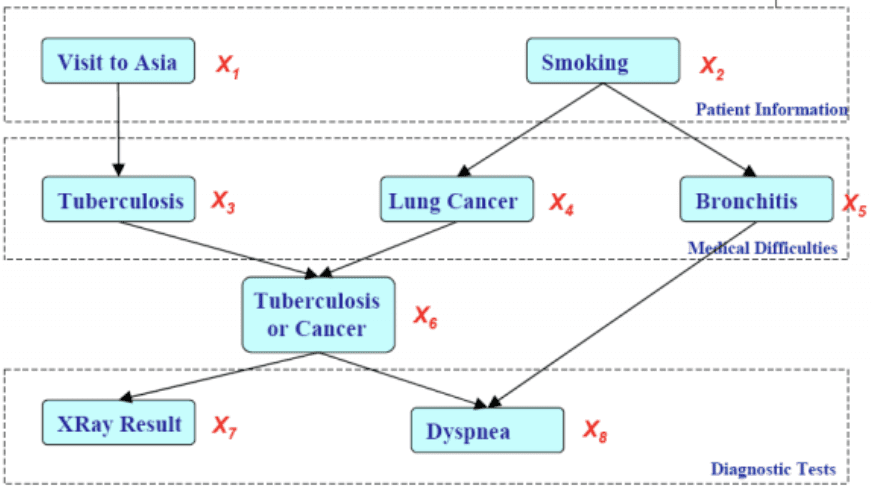
Graph diatas menunjukan hubungan sebab akibat antara variabel misalnya merokok (smoking) menyebabkan kanker paru (Lung Cancer) dan bronkitis. Kemudian tuberkolosis disebabkan oleh kunjungan ke asia dst.
P(X1,X2,X3,X4,X5,X6,X7,X8)=P(X1).P(X2).P(X3|X1).P(X4|X2).P(X5|X2).P(X6|X3,X4).P(X7|X6).P(X8|X5,X6)
Keterhubungan ini tidak ada pada NB, karena asumsi semua variabel adalah conditional independence. Untuk 8 variabel diatas dengan Bayes rules kita membutuhkan perhitungan sebanyak 2^8
Sementara dengan Bayes net kita hanya membutuhkan perhitungan sebanyak: X1,…,X8 –> 2+2+4+4+4+8+4+8=36
Untuk X1 dan X2 hanya perlu 2 probability, contohnya untuk X1 = yes, X1=no ;
Untuk X3 punya 1 parent X1 juga sehingga ada 4 probability yaitu untuk kondisi X1X3: 00, 01,10,11 ;
Untuk X6 punya 2 parent yaitu X3 dan X4 sehingga ada 8 probability untuk kondisi X3X4X6 berikut: 000,001,010, 011, 100,101,110,111
Sampai disini dulu. Insyaallah nanti akan lanjutkan dengan contoh Bayesnet lainnya pada tulisan berikutnya. Semoga Bermanfaat!
Referensi:
Mitchell, Tom. “Machine learning.” (1997): 870-877.